PROBLEMAS ENVOLVENDO P.A.
1. O trigésimo primeiro termo de uma progressão aritmética de primeiro termo 2 e razão 3 é:
2. Em uma PA, a1 = 5 e r = 4, calcule o vigésimo termo e a soma dos 20 primeiros termos desta PA:
3. Qual O número de termos de uma PA, cuja razão é 9, o primeiro termo é 4 e o último 58?
4. Sabendo que o primeiro termo de uma PA vale 21 e a razão é 7, calcule a soma dos 12 primeiros termos desta PA:
5. Numa estrada existem dois telefones instalados um no km 3 e outro no km 27. Entre eles serão colocados mais 7 telefones, mantendo-se entre dois telefones consecutivos sempre a mesma distância. determinar em quais marc quilométricos deverão ficar esses novos telefones.
6. Numa estrada existem dois telefones instalados um no km 10 e outro no km 50. Entre eles serão colocados mais 9 telefones, mantendo-se entre dois telefones consecutivos sempre a mesma distância. determinar em quais marcos quilométricos deverão ficar esses novos telefones.
7. No primeiro semestre de um dado ano, a produção mensal de uma montadora está em PA crescente. Em janeiro, a produção foi de 18000 carros e, em junho, foi de 78000 unidades. Determine a produção dessa montadora nos meses de fevereiro, março, abril e maio.
8. Na estrada que liga a entrada da fazenda Paratins até a sua sede existem duas palmeiras, uma a 12 metros da entrada e outra a 228 metros. O proprietário deseja plantar entre elas outras cinco palmeiras. Qual deve ser a distância entre dua palmeiras consecutivas se essa distância for sempre a mesma?
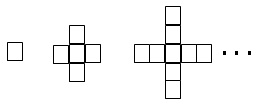
9. Observe a sequência de figuras, formadas por quadrados.
Continuando a acrescentar quadrados segundo a mesma lei, qual é o número de quadrados na 14ª figura?
10. Um pintor consegue pintar uma área de 5 m2 no primeiro dia de serviço e, a cada dia, ele pinta 2 m2 a mais do que pintou no dia anterior.
Quantos metros quadrados ele pintará no 9º dia?
Resolução de Problemas de P.A. e P.G.
1. Em uma estrada são instalados telefones SOS a cada 2,8 Km. Calcule o número de telefones instalados no trecho que vai do quilômetro 5 ao quilômetro 61, sabendo que nessas duas marcas há telefones instalados. Considere inclusive esses dois telefones.
2. No primeiro dia de abril, os operários de uma fábrica produziram 200 bicicletas. A meta era produzir em cada um dos dias seguintes desse mês 10 bicicletas a mais que no dia anterior. De acordo com essa meta:
a) Quantas bicicletas seriam produzidas no dia 20 de abril?
b) Quantas bicicletas seriam produzidas nos 20 primeiros dias de abril?
3. No projeto de uma sala de cinema, um arquiteto desenhou a planta, na forma de trapézio isósceles com a tela sobre a base menor desse trapézio. As poltronas serão dispostas em 16 fileiras paralelas às bases do trapézio, tendo 20 poltronas na primeira fileira e, a partir da segunda, cada fileira terá duas poltronas a mais que a fileira anterior. Quantas poltronas a sala terá?
4. Cinco amigos resolveram trabalhar pela eleição de um candidato a deputado federal. Para isso , cada um enviou 10 e-mails a 10 outros amigos exaltando as qualidades do candidato e pedindo que cada destinatário enviasse 10 e-mails com os mesmos dizeres a 10 novos destinatários. Suponha que cada destinatário tenha recebido um único e-mail e tenha atendido ao pedido Denominando por 1ª geração de destinatários as pessoas que receberam os e-mails desses 5 amigos; 2ª geração de destinatários as pessoas que receberam os e-mails da 1ª geração; e assim por diante, calcule o número de destinatários da 6ª geração.
5. Uma gravadora lançou no mercado um CD de música popular brasileira, e o departamento de vendas fez uma pesquisa junto às distribuidoras para verificar o número de cópias vendidas. Na primeira semana, foram vendidas 20 cópias; na segunda semana a venda dobrou em relação a primeira semana; e na terceira, dobrou em relação a segunda semana. O diretor acredita que as vendas continuarão dobrando a cada semana. Agora Responda:
a) Em que semana serão vendidas 10.240 cópias?
b) Até o final da semana indicada no item a, quantas cópias terão sido vendidas desde o lançamento do CD?
6. Em janeiro depositei R$ 100,00 no banco, em fevereiro R$ 200,00, em março R$ 300,00 e assim sucessivamente, aumentando R$ 100,00 a cada mês nos depósitos sem falhar em nenhum deles. Quanto terei depositado após quatro anos se mantiver esse mesmo procedimento?
7. Um vazamento em um tanque de gasolina provocou a perda de 2l no primeiro dia. Como o orifício responsável pelas perdas foi aumentando, no dia seguinte o vazamento foi o dobro do dia anterior. Se essa perda foi dobrando a cada dia, quantos litros de gasolina foram desperdiçados no total, após o 10º dia?
8. Em um surto epidêmico ocorrido em certa cidade com cerca de 10.000 habitantes, cada indivíduo infectado contaminava 10 outros indivíduos no período de uma semana. Supondo-se que a epidemia tenha prosseguido nesse ritmo, a partir da contaminação do primeiro indivíduo, pode-se estimar que toda a população dessa cidade ficou contaminada em, aproximadamente quantos dias?
9. (UFV) Numa caixa há 1000 bolinhas de gude. Retiram-se 15 bolinhas na primeira vez, 20 na segunda, 25 na terceira e assim sucessivamente, na mesma razão. Após a décima quinta retirada, quantas bolinhas sobrarão na caixa?
10. Um pintor consegue pintar uma área de 5 m2 no primeiro dia de serviço e, a cada dia, ele pinta 2 m2 a mais do que pintou no dia anterior. Em que dia ele terá conseguido pintar 31 m2 ?
Conteúdo retirado de livros didáticos.
Nenhum comentário:
Postar um comentário